Paxos
概述
Paxos算法是Lamport创造的基于消息的共识算法, 包括Google的Chubby 在内的很多系统都在应用Paxos算法, Google Chubby 有下面的描述
all working protocols for any asynchronous consensus we hava so far encountered hava Paxos at their core.
足见该算法在分布式系统中的地位。
背景说明
Paxos解决的问题是,在分布式系统中系统间如何就一个不可变变量达成一致,仅此而已。但是在该算法的基础之上我们可以做非常有意义的事情,比如Google Chubby就是对Multi-Paxos算法的工程实践, Multi-Paxos算法的基础就是Paxos, 通俗来说, 就是多个轮次的Paxos算法的执行,确定一系列不可变变量的值, 如果各个节点的初始状态一致,再执行相同的操作序列(即确定的一系列不可变变量的值),那么最终结果必然也是一致的。这是可以应用于系统容错和系统一致 性上的。
条件约束
在分布式系统一致性领域中有一个号称是定理的结果 FLP Impossibility, 在异步通信环境下, 没有一个算法可以保证数据一致性, 我们能够做的就是尽可能在 Liveness 和 Safety 之间找到一个平衡, 这个 CAP 理论很相像。
Paxos 做了如下保证:
Liveness
只要存在多数派,并且多数派之间网络是联通的,则:
- 肯定会有提议被接受
- 被接受的提议肯定可以被其他进程学习到
Safety
Do not be eval ! 保证不做错的事情
- 只要一个值被确定或者批准,不能出现第二个值把第一个值覆盖的情况
也是两个约束条件是 Paxos 的算法根基。
推导过程
举个栗子: 假设,三个进程 Pi、Pj 和 Pk 想就变量 V 达成一致。 最直接的想法:
P1: “进程集合中的任一进程向其他所有进程提议 V 的值,当提议被进程接收后,进程 会拒绝再次对 V 的提议”
这个想法是满足 Safety 要求的。但是问题也很明显,首先这个想法不允许任何进程故 障,这和 Liveness 要求不符合!其次如果是多个进程并发对 V 进行赋值,无法支持。
优化刚刚的想法 P1, 首先我们提出一个概念:法定集合(即进程集合中的多数派),将原 来的想法 P1 升级为
P2: “进程集合中的任一进程向其他进程提议 V 的值,当提议被法定集合采纳,即可认为 提议已经确定;当提议被进程接收后,进程会拒绝再次对 V 的提议”
其次,对于多个进程并发对 V 进程赋值的场景 P2 依然无法满足,需要将 “当提议被进程 接收后,进程会拒绝再次对 V 的提议” 这个限制去掉
P3: “进程集合中的任一进程向其他进程提议 V 的值,当提议被法定集合采纳,即可认为 提议已经确定;当提议被进程接收后,进程仍然可以接收对 V 的提议”
如果只是允许进程可以接收多次对 V 的提议,系统一致性同样也无法满足,比如 Pi.v 被 赋值为 a, 而且 Pj.v 也采纳了 a,但是同时 Pk.v 被赋值为 b,其实正常来说 v=a 已经 形成了多数派,按照 P3 的约定,这个提议可以被接受了,是不能再修改的,但是由于“当 提议被进程接收后,进程仍然可以接收对 V 的提议”,这个限制导致 Safety 无法满足, 说明 P3 存在局限性!
正常来说上面的例子中 v=a 已经被法定集合确认,它本身已经是确定性取值,Pk 已经没 有任何选择了,它只能提议 v=a.
因此,我们调整一下策略, Pk 在提议前先去向其他进程询问一下其他人的提议值,如果 所有进程 v 的值都为 null, 那就提议自己的 v=b, 如果不为空就提议某个值出现次数最多 的 那个值,回到刚刚的例子, pk 向 pi 和 pj 询问到了 v=a,此时 pk 也提议 v=a,此时所有 进程对 v=a 达成了一致。但是很不幸,恰巧每个值出现的次数相等怎么办?举例来说就 是, Pi 提议 v=a, Pj 提议 v=b, 此时 Pk 向 Pi 和 Pj 询问的结果是[v=a,1] [v=b,1] ,此时 Pk 懵逼 了,它无法判断该如何提议了。
看来,单纯依靠 v 的值作为询问依据是不行的, 那不妨给每个 v 都加一个基友 epoch 吧, 我们姑且认为 epoch 是 v 的一个身份,他是一个单调递增的数字,我们将 v 和 epoch 统称 为提案,
至此其实已经初步具备了 Paxos 的算法模型,即 Paxos 算法在正式提案前会有一个询问的 过程,其实也是一个两阶段的算法。同时我们也将进程内的角色细化一下,每个进程分为 两种角色:
Proposer 和 Acceptor。 Proposer 负责询问 Acceptor 选择一个合理的提案,并将该提案提 交给 Acceptor; Acceptor 负责接收和处理 Proposer 的询问和提案。
还是刚刚的例子:如果 Proposer 询问的结果为 null,则 Proposer 将自主的给 v 赋值, 如 果不为 null,则 Proposer 需要选择一个 v 作为提案提交。 试想如果两个 Proposer 同时询 问且结果都为 null,则都会 向各自的法定集合提交提案,两个法定集合必然存在至少一个 common Acceptor,此时 common Acceptor 如何选择这两个 Processor 的提案呢?
可以应用提案的 epoch 属性来解决这个问题,我们可以设定一个规则:common Acceptor 如果同时接收到多个提案,只会接收 epoch 最大的提案,拒绝掉其他提案。 我们假设 acceptor 使用 a.epoch 来表示 接收的 epoch 值,如果一个提案 PA 的 epoch 大于 a.epoch,Acceptor 则接收这个提案 PA 并更新自己的 a.epoch=PA.epoch ,反之拒绝掉这次提案.
假定 Pk 接收到了 Pi 和 Pj 的两个提案,且 Pi.epoch > Pj.epoch, 此时依然存在两种情形需要 分别考虑:
情形一: 如果 Pk 先收到了 Pi 的提案, 当接收到 Pj 的提案时,直接拒绝
情形二: 如果 Pk 先收到了 Pj 的提案,此时 Pk.epoch = Pj.epoch,当接收到 Pi 的提案时, 发现 Pi.epoch > pk.epoch,仍然要接收,此时显然和 Safety 冲突,因为当 Pk 接收到了 Pj 的提案时,多数派已经形成,即不可变 变量已经确定,此时不应该再接收 Pi 的提案!
其实我们期望的是,无论是 Pk 先接收到谁的提案, 结果是一致的,即:接收到 epoch 最 大的提案,拒绝掉其他提案。
那么我们能不能在询问阶段 Pi 顺便告诉 Pk,自己在提交阶段的 Epoch 呢? 在询问阶段,各个 Proposer 向 Acceptor 告知提交的 epoch, Acceptor 只接收最大的 Epoch 并记录下来,这样在提交阶段,如果 Proposer 的 epoch 小于自己的 epoch 则拒绝 这次提案
回过头继续看刚刚的情形二, 虽然 Pk 先收到了 Pj 的提案,但是由于 Pk 此时的 a.epoch = Pi.epoch,因为在询问阶段 Pk 就已经将最大的 epoch 记录,此时由于 Pk 的 a.epoch > Pj.epoch,仍然会拒绝掉 Pj
继续看刚刚导致 Pk 懵逼的那个例子,Pk 在提案前向 Pi 和 Pj 询问 v 的取值,Pi 反馈是 v=a, Pj 反馈是 v=b, 因为当时没有 epoch 的概念,导致 Pk 无法选择,此时我们已经有了 epoch 的支持,Pk 如何选择 v 的取值呢?
先说结论:选择 epoch 最大的 v 的取值
综合以上我们总结一下 Paxos 执行过程:
询问阶段(Propose 阶段)
Proposer 发送 Propose Proposer 生成全局唯一且递增的 Proposal ID,向集群的所有机器发送 Propose,这里无 需携带提案内容,只携带 Proposal ID 即可
Acceptor 应答 Propose Acceptor 收到 Propose 后,做出“两个承诺,一个应答” 两个承诺
第一,不再应答 Proposal ID 小于等于(注意:这里是 <= )当前请求的 Propose ⎫第二,不 再应答 Proposal ID 小于(注意:这里是 < )当前请求的 Accept 请求
一个应答
返回已经 Accept 过的提案中 Proposal ID 最大的那个提案的 Value 和 accepted Proposal ID,没有则返回空值
接收阶段(Accept 阶段)
Proposer 发送 Accept
“提案生成规则”:Proposer 收集到多数派的 Propose 应答后,从应答中选择存在提案 Value 的并且同时也是 Proposal ID 最大的提案的 Value,作为本次要发起 Accept 的提案。 如果所有应答的提案 Value 均为空值,则可以自己随意决定提案 Value。然后携带上当前 Proposal ID,向集群的所有机器发送 Accept 请 求
应答 Accept
Acceptor 收到 Accpet 请求后,检查不违背自己之前作出的“两个承诺”情况下,持久 化当前 Proposal ID 和提案 Value。最后 Proposer 收集到多数派的 Accept 应答后,形成 决 议
范例学习
case1:
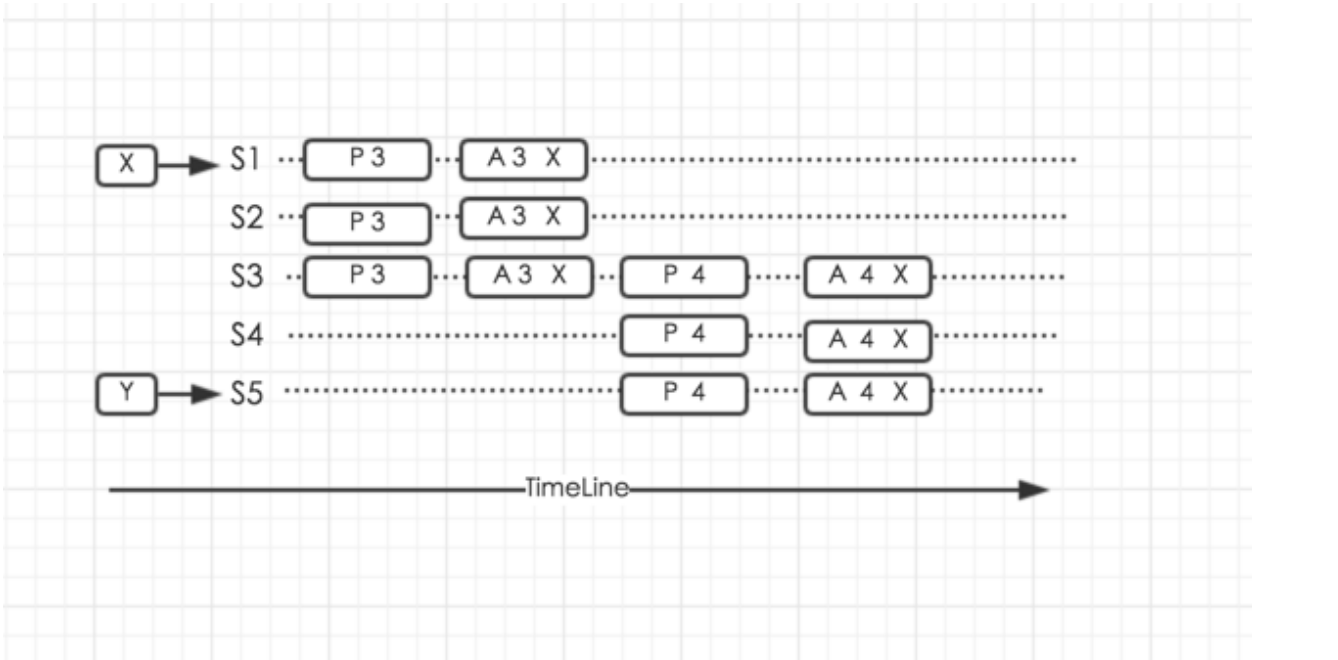
服务器 S1, 收到将 v 命名为 X 的请求, v=X,被法定集合接受。 决议已经形成,决议值 为 X。然后 P5 学习到 v=X, 并接受它。
case2:
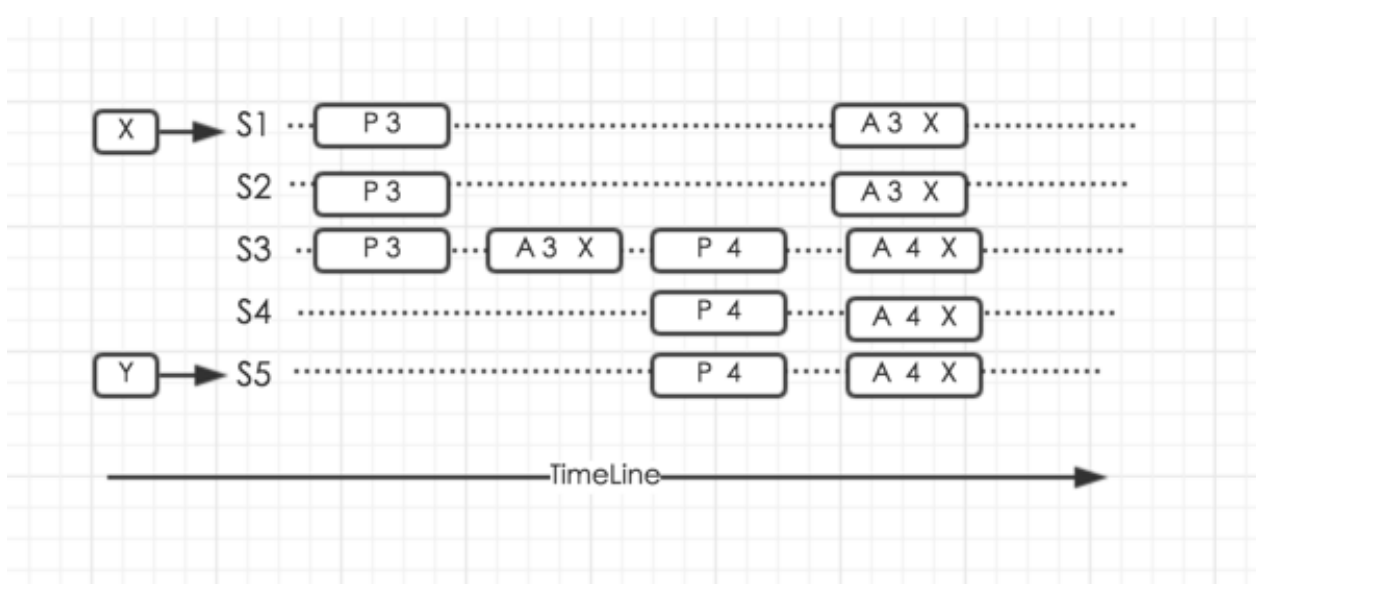
v=x 只被 S3 接收了,它被 P4 学习到了,并被法定集合接收。
case3:
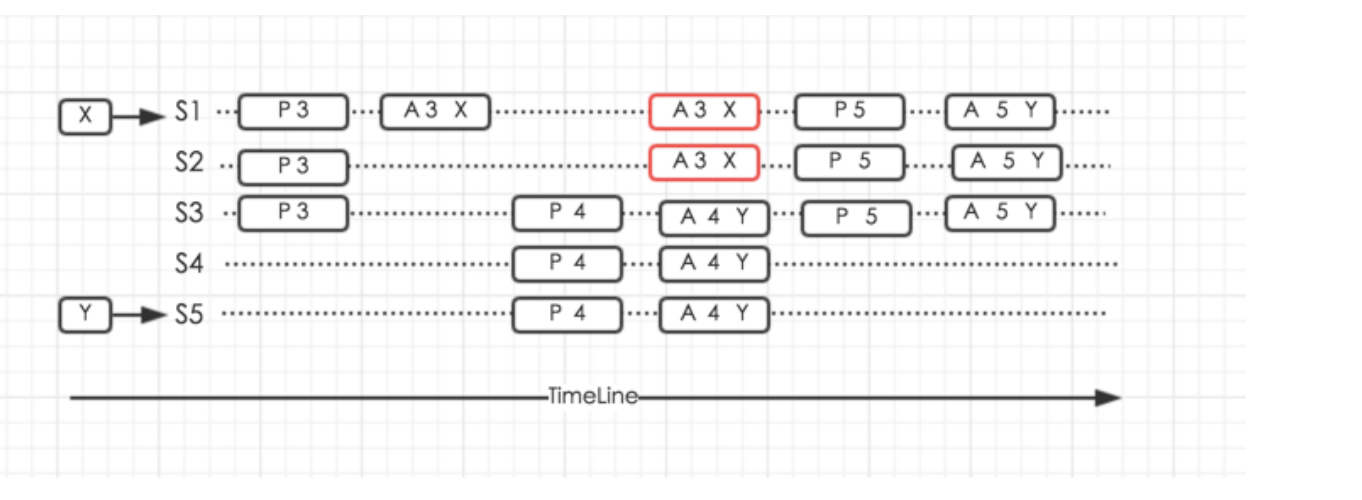
P 3 没有被多数派 Accept(只有 S1 Accept),同时也没有被 P 4 学习到。由于 P 4 Propose 的所 有应答,均未返回 Value,则 P 4.5 可以 Accept 自己的 Value(Y) 后续 P 3 的 Accept(X)会失败,进行下一轮提案,最终 S1,S2 的 Acceptor 也学习到了 Value(Y)
引用
[1] The Chubby lock service for loosely-coupled distributed systems (PDF)
[2] https://en.wikipedia.org/wiki/Consensus_(computer_science)
[3] http://blog.csdn.net/chen77716/article/details/27963079
[4]https://www.zhihu.com/question/19787937/answer/82340987
[5] http://research.microsoft.com/en-us/um/people/lamport/pubs/paxos-simple.pdf
[6] https://www.zhihu.com/question/19787937
[7] http://oceanbase.org.cn/?p=90
[8] https://zhuanlan.zhihu.com/p/20417442引用
